As Eric Walker — the real inventor of “moneyball” — puts it, “moneyball is about seeking undervalued commodities.” Perhaps baseball teams have done a better job of acquiring undervalued commodities since the publication of Michael Lewis’s Moneyball in 2003. But arbitrage opportunities are fleeting, as the price of a “bargain” is driven up and it is no longer a “bargain.” Moreover, as Walker explains, “moneyball” has been around since the 1980s and the concept surely had some influence on player selection even before Lewis made it famous.

At any rate, I have analyzed the performance and payrolls of American League (AL) teams for 1988-2011 to determine their effects on teams’ won-lost (W-L) records. I focused on the AL because an analysis of both major leagues would have been complicated by the presence of the designated hitter in the AL and the absence of the DL in the National League. I began with 1988 because that is the first year covered by the USATODAY Salaries Database for baseball. Performance data are from Retrosheet.

What did I learn from those 24 years’ worth of data? This:

1. Payroll does not drive W-L record.

2. Payroll is mainly determined by 7 aspects of performance.

3. W-L record is mainly determined by 9-11 aspects of performance, only 2-4 of which overlap with the determinants of payroll.

4. W-L record is strongly correlated with the ratio of runs scored (RS) to runs allowed (RA), with an r-squared of 0.89. There is considerable overlap between the determinants of RS-RA and the determinants of W-L record. There is not much overlap between the determinants of RS:RA and the determinants of payroll.

I begin with the relationship between payroll and W-L record:

 Payroll index is the ratio of a team’s payroll in a given season to the average payroll of all AL teams in the same season. A regression on W-L record with payroll index as an explanatory variable cannot include additional explanatory variables that are statistically significant (less than 1 percent chance of a random relationship with the dependent variable). As discussed below, this result indicates that payroll index is a proxy for measures of performance that are statistically significant determinants of a W-L record and RS:RA.

The following table summarizes the results of six regressions. Instead of showing the coefficients for the explanatory variables, I have converted them to elasticities, expressed as the percentage increase in a dependent variable that results from a 1-percent increase in the value of the explanatory variable.

Before I walk through the table, I should observe that the figures represent average tendencies over a 24-year span. The figures are significant, but they do not necessarily indicate the best course of action for a given team in a given situation. The best  course of action for a given team in a given situation will depend on the team’s options (e.g., players available on the free-agent market), on the likely payoff of those options (e.g., addition to runs scored if player A is signed and player B is traded away), and on the cost of obtaining each payoff (e.g., net addition to payroll if player A is signed and player B is traded).

The results in the payroll index column show that the payrolls of AL teams in 1988-2011 were driven mainly by batters’ on-base percentage (OBP); pitchers’ avoidance of giving up home runs; pitchers’ ability to strike out batters (SO); fielders’ avoidance of errors (ERR); batters’ home runs (HR); catchers’ throwing out base stealers (CS); and batters’ not hitting a lot of triples (3B) — perhaps because of the typical characteristics of triples hitters (e.g., they are not usually home-run hitters).

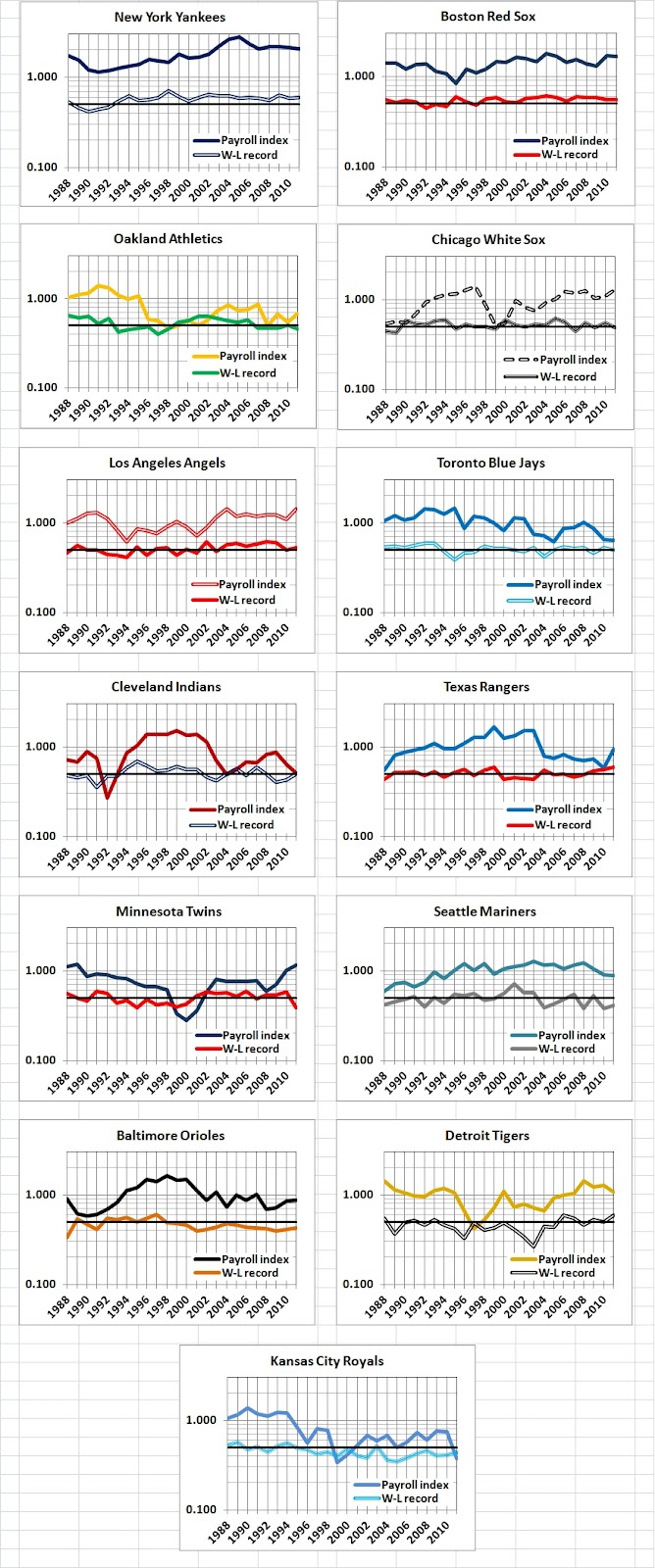
In the next column we see, again, that payroll spending — in the aggregate over 24 seasons — does not strongly influence W-L record. But because payroll is a proxy for several performance variables, no other variable show up as statistically significant when payroll index is used as an explanatory variable. It is important to note, however, that the relatively weak relationship between W-L record and payroll index for the entire AL masks considerable variation across teams. Here is a summary comparison, for the 13 teams that were in the AL in every year from 1988 through 2011:

The Oakland A’s of “moneyball” fame did will for the amount of money spent on payroll, as measured by W-L record divided by payroll index (right-hand column). But, on that measure, the A’s did no better than the Twins, and not a lot better than the Royals and White Sox.

The Yankees were the best team in the AL during 1988-2011, and they paid what it took to be the best. The Red Sox were the second-best team, and they paid accordingly. After that, results were mixed. The A’s paid a lot less than the Yankees and Red Sox, and still won a lot — but did not get much in return when they spent more (correlation coefficient of 0.19, as against 0.50 for the Yankees and 0.31 for the Red Sox). Though an above-average payroll index was not required for a winning record, four of the top six team in W-L and every team with a payroll index of 1.00 or grater had a winning record. All teams but one — the Rangers — managed to eke out some additional wins by increasing their payrolls.

The following graphs illustrate several story lines, such as success with young, low-priced players who then become higher-priced and less-productive players; overspending on once-outstanding veterans whose best seasons were behind them; overspending on promising players whose performance did not rise with their salaries. For ease of reading each team’s W-L record, I have inserted in each graph a horizontal black line at the break-even mark (.500).

Seen in the context of 13 team histories, the A’s look like a team that did well for a while with relatively high-priced players; pared its payroll as its fortunes faded; happened to do well for a while on low-priced players, and then faded as its payroll rose.

Let us now to the column headed W-L record (II) in the first table above. This is where the bat meets the ball, so to speak, because it tells us something about the aspects of performance that determine a team’s W-L record. Except for on-base percentage (OBP), the determinants of payroll have little to do with winning. Defense (represented in fielding average) is far and away the most important determinant of winning. (The payoff of defense may be somewhat overstated, as I will come to.) After that, preventing hits (H) and getting them weigh heavily. Pitchers who save games (SV) are important to winning, as are pitchers who do not give up a lot of walks (BB). Home runs (HR) are just as important as payroll, even though they are down the list of factors that determine payroll.

As mentioned earlier, W-L record is strongly correlated with the ratio of runs scored to runs allowed (RS:RA). The next two columns of the table assess the relationships between RS and various measures of performance; the right-hand column deals with RA. On the offensive side, HR remains important, as does OBP appear, directly and in the form of key elements — H, BA, and BB. On the defense side, fielding is key (more below). Next are H, BB, and HR allowed by pitchers, meaning that allowing relatively few H, BB, and HR are keys to the defensive side of the game. Another key, though a less important one, is striking out batters (SO).

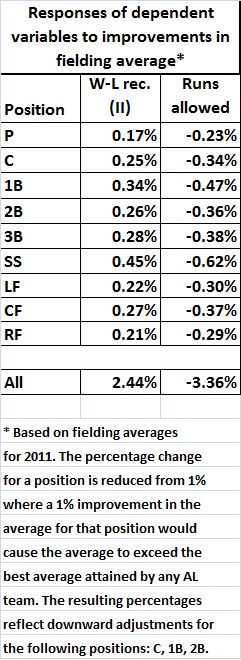
As for fielding, a position-by-position view is more relevant, and the possibility of obtaining better fielding is overstated for some positions. The following table affords the position-by-position view and eliminates the overstatements:

What this tells us is that improved fielding, at any position, can strongly improve a team’s chances of winning, even though fielding is not among the key determinants of payroll.

Rumor has it that the Yankees have offered Derek Jeter a three-year contract worth $45 million. The annual rate of $15 million would be a comedown from Jeter’s 2010 pay of $22.6 million (source), but in terms of on-field performance, Jeter would be grossly overpaid. And he wants to be more grossly overpaid, of course.

Let’s look at Jeter’s value to the Yankees since 1996, the first year for which his salary is known:

						OPS+ per
Year	Age	OPS+		Salary		$10 mn
1996	22	101		$130,000		0.07769
1997	23	103		$550,000		0.01873
1998	24	127		$750,000		0.01693
1999	25	153		$5,000,000		0.00306
2000	26	128		$10,000,000		0.00128
2001	27	123		$12,600,000		0.00098
2002	28	111		$14,600,000		0.00076
2003	29	125		$15,600,000		0.00080
2004	30	114		$18,600,000		0.00061
2005	31	125		$19,600,000		0.00064
2006	32	132		$20,600,000		0.00064
2007	33	121		$21,600,000		0.00056
2008	34	102		$21,600,000		0.00047
2009	35	125		$21,600,000		0.00058
2010	36	90		$22,600,000		0.00040
		119		$205,430,000		0.00087

OPS+ is a measure of offensive performance. It is on-base percentage plus slugging average (OPS) adjusted for year and ballpark. An OPS+ of 100 represents the average for the league and year.

Jeter’s on-field value to the Yankees, as an offensive player, peaked in 1999, when his OPS+ reached a career-high 153. His OPS+ per $10 million of salary in that year was 0.00306. It has been all downhill since, both in terms of OPS+ (though there have been some good years since 1999) and OPS+ per $10 million of salary. The latter figure dwindled to 0.00040 in 2010, when Jeter’s OPS+ fell to 90, that is, 90 percent of the league average.

It is only reasonable to assume that Jeter’s productivity will decline further from its peak, even if he recovers somewhat from the 2010’s unusually weak performance. Even at $15 million per season, Jeter will be an over-priced commodity, given his likely on-field performance.

So, if Jeter is worth $15 million a year, or more, it’s only because of his leadership qualities (which can’t be measured) and his draw as a symbol of Yankee greatness. I suspect that Jeter’s leadership qualities will not be enough to reverse the Yankees’ evident decline. Further, that decline will more than offset whatever value Jeter has at the box office.

I look forward, with sadness, to some relatively lean years in the Bronx, and to buyer’s remorse on the part of the Yankees if they settle with Jeter for much more than $15 million a season.

SUPERSEDED BY “THE AMERICAN LEAGUE’S GREATEST HITTERS: III“

UPDATED 12/08/11

When last seen, the best of the American League’s greatest hitters were:

Adjusted	Nominal	Player	Years in AL		Batting average		% change	# change
rank*	rank	(all-caps, Hall of Fame;	From	To	Nominal	Adjusted	in BA	in rank
		* indicates active)
1	12	Ichiro Suzuki*	2001	2010	.331	.353	6.2%	11
2	1	TY COBB	1905	1928	.366	.353	-3.9%	-1
3	2	Shoeless Joe Jackson	1908	1920	.356	.351	-1.3%	-1
4	10	NAP LAJOIE	1901	1916	.336	.333	-0.9%	6
5	3	TRIS SPEAKER	1907	1928	.345	.331	-4.0%	-2
6	16	ROD CAREW	1967	1985	.328	.331	0.9%	10
7	11	EDDIE COLLINS	1906	1930	.333	.326	-2.2%	4
8	6	BABE RUTH	1914	1934	.343	.324	-6.1%	-2
9	8	LOU GEHRIG	1923	1939	.340	.323	-5.4%	-1
10	18	JOE DIMAGGIO	1936	1951	.325	.322	-0.7%	8
11	4	TED WILLIAMS	1939	1960	.344	.319	-7.9%	-7
12	15	WADE BOGGS	1982	1999	.328	.319	-2.8%	3

I left the earlier post hanging on the question of how the top hitters would compare when their batting averages were adjusted further, for age. I now have some of the answers.

To get the answers, I quantified the relationship between adjusted batting average and age for the 120 hitters considered in the earlier post. (As a reminder, those hitters attained nominal lifetime averages of .285 or better in at least 5,000 plate appearances in the American League. Their averages take into account long-term and year-to-year changes in playing conditions, as well as differences among ballparks at a give time and over time.) Here is the relationship, in graphical form:

I used the equation shown on the graph to adjust each hitter’s annual batting average according to the age at which he attained the average. If the “normal” hitter peaks at 28, as the equation suggests, averages attained before and after the age of 28 are “understated.” That is, if a player hits .300 at the age of 20, that’s equivalent to hitting .315 at the age of 28; and if a player hits .300 at the age of 40, that’s equivalent to hitting .341 at the age of 28.

My analysis of age-adjusted batting average has yielded two key findings, thus far. The first finding, which is captured in the following graph and its accompanying table, is that the top averages for ages 18-41 were accomplished by just seven different players. This graph compares the year-by-year, age-adjusted averages for each of the seven players:

For ease of viewing, I omitted the five players (Speaker, Carew, Collins, Ruth, and Gehrig) who never hold the top spot at any age, despite their impressive career averages. The top hitters at each age are as follows:

		Age-adjusted
Age	Player	BA
18	Cobb	.267
19	Cobb	.336
20	Cobb	.369
21	Jackson	.392
22	Cobb	.395
23	Cobb	.399
24	Cobb	.387
25	Cobb	.397
26	Cobb	.391
27	Cobb	.380
28	Cobb	.379
29	Lajoie	.383
30	Cobb	.396
31	Cobb	.387
32	Cobb	.369
33	Suzuki	.377
34	DiMaggio	.362
35	Lajoie	.414
36	Suzuki	.364
37	Lajoie	.373
38	Williams	.398
39	Williams	.343
40	Cobb	.357
41	Boggs	.343

Given that information, it shouldn’t surprise you to learn that Ty Cobb returns to the top of the heap when his single-season averages are age-adjusted, and weighted by his at-bats in each season, to obtain an age-adjusted lifetime average. Here is the age-adjusted list of top-12 career batting averages:

	Batter	Age-adjusted career BA
1	Ty Cobb	.3639
2	Shoeless Joe Jackson	.3559
3	Ichiro Suzuki*	.3582
4	Nap Lajoie	.3405
5	Tris Speaker	.3313
6	Rod Carew	.3307
7	Ted Williams	.3306
8	Eddie Collins	.3258
9	Babe Ruth	.3236
10	Lou Gehrig	.3228
11	Joe DiMaggio	.3223
12	Wade Boggs	.3190
	* Through 2010 season; before .272 average in 2011 reduced career BA by .0054.

I have not extended my analysis to include the 2011 season, but it is clear that Suzuki now belongs in 3rd place. The loss of .0054 from his nominal career BA in 2011 is far greater than his age-adjusted lead (.0023) over Jackson through 2010.

Through a painstaking series of adjustments for changes in playing standards and conditions, and for differences among ballparks, I have reassessed the single-season and career batting averages of the American League’s top hitters. The reassessment covers 120 players whose career average in the American League is at least .285 in at least 5,000 plate appearances.

I will devote a future post to a detailed explanation of the adjustments. In this post, I give an overview of the adjustments and present a revised ranking of the 120 players. I also discuss — but do not adjust for — the effects of age on the revised batting averages and relative standing of players.

I make three kinds of adjustments to nominal (official) BA. One adjustment is a time constant, which captures gradual changes from 1901 to the present that have worked against batters. Such changes would be the improvement of fielding gloves (which have made it harder to get hits, while also raising fielding averages), the introduction of night baseball, and the gradual increase in proportion of games played at night.

A second adjustment is an annual factor that captures the up-and-down swings in the relative difficulty of hitting. These swings have occurred because of changes in the ball, the frequency of its replacement, the size of the strike zone, and the height of the pitching mound, and perhaps other factors.

A third adjustment — one that is unique to each team-park combination — reflects the relative ease or difficulty of hitting in the various parks that have been used in the American League. In many cases the adjustment factor for a given park changes during the years of its use because of significant changes in the dimensions of the field.

The following graph combines the effects of the first two adjustments into a single number for each season. A value greater than 1 means that each hitter’s nominal average for that season was increased to some degree. A value less than 1 means that each hitter’s average for that season was decreased to some degree.

The largest upward adjustments affect averages compiled in the “deadball” years of 1902-1909 and 1913-1916, and in the “era of the pitcher,” from 1962 through 1975. The largest downward adjustments affect averages compiled in the first two years of the AL’s existence and the “lively” ball era, which — judging from the numbers — began in 1919 and lasted through 1938.

The final adjustments — for differences in parks — range widely. For example, Red Sox hiiters (including Ted Williams) suffered a penalty of 5.9 percent for the 1934-2010 seasons, when Fenway Park acquired its present dimensions. By contrast, Yankees who played in the original Yankee Stadium from 1923 through 1973 earned a boost of 4 percent because the original park (despite its short foul lines) was inimical to batters (including Joe DiMaggio).

The following graph captures the total effect of the three adjustments. Each point represents one of the 120 hitters.

The pattern, which the curved line emphasizes, is consistent with the adjustments summarized in the first graph. The points don’t fall neatly on the curved line for three reasons: (1) variations in the length of players’ careers, (2) variations in the numbers of at-bats across seasons (and thus in the weight attached to a season in compiling a career average), and (3) the park-adjustment factor, which varies widely from park to park and (sometimes) for a particular park, if its configuration changed significantly.

How did the various adjustments affect the rankings? First, as would be expected because of the inflation of batting averages in the 1920s and 1930s, those decades are over-represented among the 120 hitters, as shown in the following table. (“Median year” refers to the decade in which a player’s median year occurs. For example, Ty Cobb’s career spanned 1905-1928, so he is counted as a member of the 1911-1920 decade in the following table and the one after it.)

Distribution of Hitters, by Decade
	Median year	Number	Percent
	1901-1910	2	1.7%
	1911-1920	7	5.8%
	1921-1930	17	14.2%
	1931-1940	21	17.5%
	1941-1950	8	6.7%
	1951-1960	8	6.7%
	1961-1970	3	2.5%
	1971-1980	8	6.7%
	1981-1990	10	8.3%
	1991-2000	22	18.3%
	2001-2010	14	11.7%
		120	100%

The adjustments to nominal batting averages did a good job of rectifying the bias toward players of the 1920s and 1930s:

	Average Rank, by Decade
	Median year	Nominal	Adjusted	Change*
	1901-1910	28	17	11
	1911-1920	22	23	-1
	1921-1930	29	65	-36
	1931-1940	44	83	-39
	1941-1950	60	63	-3
	1951-1960	84	54	30
	1961-1970	83	43	40
	1971-1980	86	49	37
	1981-1990	79	52	27
	1991-2000	79	64	15
	2001-2010	58	79	-21
	* Positive number represents improvement (higher average rank); negative number represents slippage (lower average rank).

Until someone convinces me otherwise, I conclude that the top hitters of the “deadball” era really were great by comparison with those who came later. They are not alone at the top, however. Among the top 10 in the following table are a contemporary player (Ichiro Suzuki), a player of recent memory (Rod Carew), and three Yankees who enjoyed great years in the 1920s and 1930s (Babe Ruth, Lou Gehrig, and Joe DiMaggio). Here, then, are all 120 hitters, listed in the order of adjusted rank:

Adjusted	Nominal	Player	Years in AL		Batting average		% change	# change
rank*	rank	(all-caps = Hall of Fame; asterisk =	From	To	Nominal	Adjusted	in BA	in rank
		active)
1	12	Ichiro Suzuki*	2001	2010	.331	.353	6.2%	11
2	1	TY COBB	1905	1928	.366	.353	-3.9%	-1
3	2	Shoeless Joe Jackson	1908	1920	.356	.351	-1.3%	-1
4	10	NAP LAJOIE	1901	1916	.336	.333	-0.9%	6
5	3	TRIS SPEAKER	1907	1928	.345	.331	-4.0%	-2
6	16	ROD CAREW	1967	1985	.328	.331	0.9%	10
7	11	EDDIE COLLINS	1906	1930	.333	.326	-2.2%	4
8	6	BABE RUTH	1914	1934	.343	.324	-6.1%	-2
9	8	LOU GEHRIG	1923	1939	.340	.323	-5.4%	-1
10	18	JOE DIMAGGIO	1936	1951	.325	.322	-0.7%	8
11	4	TED WILLIAMS	1939	1960	.344	.319	-7.9%	-7
12	15	WADE BOGGS	1982	1999	.328	.319	-2.8%	3
13	47	Don Mattingly	1982	1995	.307	.318	3.3%	34
14	74	MICKEY MANTLE	1951	1968	.298	.317	6.0%	60
15	7	HARRY HEILMANN	1914	1929	.342	.315	-8.9%	-8
16	30	Derek Jeter*	1995	2010	.314	.314	0.1%	14
17	5	GEORGE SISLER	1915	1928	.344	.313	-9.8%	-12
18	36	Edgar Martinez	1987	2004	.312	.312	0.1%	18
19	25	KIRBY PUCKETT	1984	1995	.318	.311	-2.1%	6
20	89	EDDIE MURRAY	1977	1997	.295	.311	5.1%	69
21	99	Thurman Munson	1969	1979	.292	.310	6.1%	78
22	53	PAUL MOLITOR	1978	1998	.306	.310	1.2%	31
23	35	Magglio Ordonez*	1997	2010	.312	.310	-0.6%	12
24	31	Harvey Kuenn	1952	1960	.313	.309	-1.4%	7
25	44	Roberto Alomar	1991	2004	.309	.308	-0.4%	19
26	9	AL SIMMONS	1924	1944	.337	.308	-9.3%	-17
27	17	EARLE COMBS	1924	1935	.325	.308	-5.6%	-10
28	68	Minnie Minoso	1949	1964	.300	.307	2.4%	40
29	70	Joe Judge	1915	1934	.299	.307	2.7%	41
30	45	SAM CRAWFORD	1903	1917	.309	.307	-0.5%	15
31	55	Tony Oliva	1962	1976	.304	.307	0.7%	24
32	92	Mickey Rivers	1970	1984	.295	.306	3.7%	60
33	38	Baby Doll Jacobson	1915	1927	.311	.305	-1.9%	5
34	83	Carl Crawford*	2002	2010	.296	.305	2.8%	49
35	67	Julio Franco	1983	1999	.301	.304	1.3%	32
36	54	GEORGE BRETT	1973	1993	.305	.304	-0.3%	18
37	56	Paul O’Neill	1993	2001	.303	.304	0.1%	19
38	48	HOME RUN BAKER	1908	1922	.307	.303	-1.2%	10
39	72	Cecil Cooper	1971	1987	.298	.303	1.7%	33
40	20	SAM RICE	1915	1934	.322	.303	-6.2%	-20
41	14	HEINIE MANUSH	1923	1936	.331	.303	-9.1%	-27
42	32	BILL DICKEY	1928	1946	.313	.303	-3.3%	-10
43	101	Lou Piniella	1964	1984	.291	.302	3.9%	58
44	29	Cecil Travis	1933	1947	.314	.302	-3.9%	-15
45	103	Carney Lansford	1978	1992	.290	.302	4.1%	58
46	41	LUKE APPLING	1930	1950	.310	.302	-2.8%	-5
47	50	Stuffy McInnis	1909	1922	.307	.302	-1.7%	3
48	114	Bill Skowron	1954	1967	.286	.301	5.2%	66
49	98	Luis Polonia	1987	2000	.292	.301	3.0%	49
50	84	Garret Anderson	1994	2008	.296	.301	1.5%	34
51	79	AL KALINE	1953	1974	.297	.300	0.9%	28
52	52	GEORGE KELL	1943	1957	.306	.300	-2.2%	0
53	34	Manny Ramirez*	1993	2010	.312	.300	-4.1%	-19
54	81	Bernie Williams	1991	2006	.297	.299	0.7%	27
55	64	Frank Thomas	1990	2008	.301	.299	-0.8%	9
56	13	JIMMIE FOXX	1925	1942	.331	.298	-11.1%	-43
57	97	Mike Hargrove	1974	1985	.292	.298	1.8%	40
58	42	Bobby Veach	1912	1925	.310	.298	-4.2%	-16
59	60	Alex Rodriguez*	1994	2010	.303	.297	-2.0%	1
60	91	Kevin Seitzer	1986	1997	.295	.297	0.6%	31
61	105	John Olerud	1989	2005	.289	.297	2.5%	44
62	102	NELLIE FOX	1947	1963	.290	.297	2.2%	40
63	107	Wally Joyner	1986	2001	.289	.296	2.4%	44
64	104	Harold Baines	1980	2001	.289	.296	2.2%	40
65	112	Carlos Guillen*	1998	2010	.286	.296	3.2%	47
66	116	ROBIN YOUNT	1974	1993	.285	.295	3.4%	50
67	119	Gene Woodling	1946	1962	.284	.295	3.6%	52
68	90	LOU BOUDREAU	1938	1952	.295	.294	-0.3%	22
69	111	Raul Ibanez	1996	2008	.286	.294	2.8%	42
70	120	YOGI BERRA	1946	1963	.284	.294	3.5%	50
71	86	Kenny Lofton	1992	2007	.296	.293	-1.0%	15
72	23	HANK GREENBERG	1930	1946	.319	.293	-8.8%	-49
73	93	Albert Belle	1989	2000	.295	.293	-0.8%	20
74	94	Pete Runnels	1951	1962	.294	.292	-0.7%	20
75	82	Shannon Stewart	1995	2008	.297	.292	-1.5%	7
76	66	Ivan Rodriguez	1991	2009	.301	.292	-3.0%	-10
77	110	Mickey Vernon	1939	1958	.287	.292	1.8%	33
78	95	Hal McRae	1973	1987	.293	.292	-0.4%	17
79	96	Tony Fernandez	1983	2001	.293	.292	-0.4%	17
80	115	Miguel Tejada*	1997	2010	.286	.292	2.0%	35
81	22	MICKEY COCHRANE	1925	1937	.320	.291	-10.0%	-59
82	78	Mike Sweeney	1995	2010	.298	.291	-2.4%	-4
83	21	CHARLIE GEHRINGER	1924	1942	.320	.290	-10.5%	-62
84	80	Buddy Lewis	1935	1949	.297	.290	-2.5%	-4
85	49	George Burns	1914	1929	.307	.289	-6.2%	-36
86	26	GOOSE GOSLIN	1921	1938	.316	.289	-9.4%	-60
87	58	Mike Greenwell	1985	1996	.303	.288	-5.1%	-29
88	51	Johnny Pesky	1942	1954	.307	.287	-6.7%	-37
89	24	EARL AVERILL	1929	1940	.318	.287	-10.8%	-65
90	88	Juan Gonzalez	1989	2005	.295	.287	-3.0%	-2
91	43	John Stone	1928	1938	.310	.287	-8.0%	-48
92	19	Ken Williams	1918	1929	.324	.286	-13.1%	-73
93	100	Ken Griffey	1989	2010	.291	.286	-1.8%	7
94	65	Billy Goodman	1947	1961	.301	.286	-5.2%	-29
95	28	Bibb Falk	1920	1931	.314	.286	-10.0%	-67
96	113	Willie Wilson	1976	1992	.286	.286	0.0%	17
97	108	Rafael Palmeiro	1989	2005	.288	.285	-0.8%	11
98	59	Buddy Myer	1925	1941	.303	.285	-6.1%	-39
99	69	Michael Young*	2000	2010	.300	.285	-5.3%	-30
100	73	JIM RICE	1974	1989	.298	.285	-4.6%	-27
101	39	Bob Meusel	1920	1929	.311	.285	-9.2%	-62
102	46	Gee Walker	1931	1941	.307	.283	-8.6%	-56
103	62	Ben Chapman	1930	1941	.302	.282	-7.1%	-41
104	27	Jack Tobin	1916	1927	.315	.282	-11.5%	-77
105	117	Alan Trammell	1977	1996	.285	.282	-1.2%	12
106	76	Mo Vaughn	1991	2000	.298	.281	-5.8%	-30
107	106	Chuck Knoblauch	1991	2002	.289	.281	-2.7%	-1
108	33	JOE SEWELL	1920	1933	.312	.281	-11.0%	-75
109	37	Bing Miller	1921	1936	.311	.281	-10.9%	-72
110	85	Bob Johnson	1933	1945	.296	.280	-6.0%	-25
111	109	Johnny Damon*	1995	2010	.287	.280	-2.8%	-2
112	118	CARL YASTRZEMSKI	1961	1983	.285	.279	-2.2%	6
113	61	Hal Trosky	1933	1946	.302	.278	-8.6%	-52
114	40	Joe Vosmik	1930	1944	.311	.278	-11.6%	-74
115	71	Sam West	1927	1942	.299	.276	-8.2%	-44
116	77	Pete Fox	1933	1945	.298	.276	-8.0%	-39
117	75	Dom DiMaggio	1940	1953	.298	.276	-8.1%	-42
118	63	JOE CRONIN	1928	1945	.302	.275	-9.7%	-55
119	87	Doc Cramer	1929	1948	.296	.274	-7.9%	-32
120	57	Charlie Jamieson	1915	1932	.303	.274	-10.8%	-63
* The adjusted rank considers only the 120 players listed here. Players not listed could outrank some of the players near the bottom of the list.

The names of Hall-of-Famers are capitalized to draw your attention to several who were enshrined mainly on the strength of grossly inflated batting averages.

There is more work to be done, especially with respect to age. Consider, for example, Shoeless Joe Jackson, whose career ended at age 30. Had Jackson continued to play until he was 40, say, his career average would have declined, and with it his position on the list.

Ichiro Suzuki didn’t play in the U.S. until he was 27. Would his career average be even higher if he had crossed over the Pacific in his early 20s? He is atop the list because of his post-32 performance, relative to Ty Cobb’s.

Then there is the case of Ted Williams, whose average and ranking slipped markedly because he enjoyed the friendly confines of Fenway Park. But Williams, who also hit well in his “old age,” missed a lot of peak batting time during WWII and the Korean War.

I will end, for now, with this tantalizing comparison of Suzuki, Cobb, Jackson, and Williams:

Cobb’s consistent brilliance from age 22 to age 32 borders on the amazing. Williams was a great “old” hitter, as Suzuki is proving to be. It is evident that Jackson, despite the closeness of his average to Cobb’s, probably wouldn’t have caught Cobb, unless he had finished in a Suzuki-like manner.

ADDENDUM:

Final, age-adjusted BA for the top-3 all-time AL hitters:

Cobb	0.363919
Suzuki	0.358241
Jackson	0.355946

Go here for details.

Thanks to Baseball-Reference.com, I have compiled the following table:

Managers with at least 1000 wins after 1900, sorted by W-L record
	Yrs	From	To	G	W	L	W-L% ▾
Joe McCarthy	24	1926	1950	3487	2125	1333	.615
Billy Southworth	13	1929	1951	1770	1044	704	.597
John McGraw	33	1899	1932	4769	2763	1948	.586
Al Lopez	17	1951	1969	2425	1410	1004	.584
Earl Weaver	17	1968	1986	2541	1480	1060	.583
Fred Clarke	19	1897	1915	2829	1602	1181	.576
Davey Johnson	14	1984	2000	2039	1148	888	.564
Steve O’Neill	14	1935	1954	1879	1040	821	.559
Walter Alston	23	1954	1976	3658	2040	1613	.558
Bobby Cox	29	1978	2010	4508	2504	2001	.556
Miller Huggins	17	1913	1929	2570	1413	1134	.555
Billy Martin	16	1969	1988	2267	1253	1013	.553
Charlie Grimm	19	1932	1960	2368	1287	1067	.547
Sparky Anderson	26	1970	1995	4030	2194	1834	.545
Hughie Jennings	16	1907	1925	2203	1184	995	.543
Danny Murtaugh	15	1957	1976	2068	1115	950	.540
Leo Durocher	24	1939	1973	3739	2008	1709	.540
Joe Cronin	15	1933	1947	2315	1236	1055	.540
Joe Torre	29	1977	2010	4329	2326	1997	.538
Tony LaRussa	32	1979	2010	4934	2638	2293	.535
Whitey Herzog	18	1973	1990	2409	1281	1125	.532
Tom Lasorda	21	1976	1996	3041	1599	1439	.526
Bill McKechnie	25	1915	1946	3647	1896	1723	.524
Red Schoendienst	14	1965	1990	1999	1041	955	.522
Clark Griffith	20	1901	1920	2918	1491	1367	.522
Dusty Baker	17	1993	2010	2690	1405	1284	.522
Dick Williams	21	1967	1988	3023	1571	1451	.520
Jack McKeon	15	1973	2005	1952	1011	940	.518
Lou Piniella	23	1986	2010	3548	1835	1713	.517
Ralph Houk	20	1961	1984	3157	1619	1531	.514
Frankie Frisch	16	1933	1951	2246	1138	1078	.514
Bobby Valentine	15	1985	2002	2189	1117	1072	.510
Chuck Dressen	16	1934	1966	1990	1008	973	.509
Casey Stengel	25	1934	1965	3766	1905	1842	.508
Mike Hargrove	16	1991	2007	2363	1188	1173	.503
Felipe Alou	14	1992	2006	2054	1033	1021	.503
Wilbert Robinson	19	1902	1931	2819	1399	1398	.500
Art Howe	14	1989	2004	2266	1129	1137	.498
Jim Leyland	19	1986	2010	3013	1493	1518	.496
Chuck Tanner	19	1970	1988	2738	1352	1381	.495
Bruce Bochy	16	1995	2010	2574	1274	1300	.495
Bucky Harris	29	1924	1956	4410	2158	2219	.493
Lou Boudreau	16	1942	1960	2404	1162	1224	.487
Connie Mack	53	1894	1950	7755	3731	3948	.486
John McNamara	19	1969	1996	2395	1160	1233	.485
Bill Rigney	18	1956	1976	2561	1239	1321	.484
Jim Fregosi	15	1978	2000	2123	1028	1095	.484
Gene Mauch	26	1960	1987	3942	1902	2037	.483
Tom Kelly	16	1986	2001	2386	1140	1244	.478
Jimmy Dykes	21	1934	1961	2962	1406	1541	.477
Frank Robinson	16	1975	2006	2242	1065	1176	.475

Provided by Baseball-Reference.com: View Original Table
Generated 10/6/2010.

I will take a stab at assessing the “greatness” of the top ten in a future post.

Here:

The Yankees’ season didn’t fall apart until September 5. Despite some ups and downs, the Yankees’ season record stood at .632 after the game of Saturday, September 4. At that point, the Yankees had a lead of 2.5 games — their largest lead since July 26.

And then the bottom dropped out. The Yankees went 9-17 (.346) in the last four weeks of the season, finishing second in the AL East, with a final record of .586. The “stretch drive” was just too much for New York’s aging position players and shaky pitching staff.

UPDATED

The Yankees’ recent record [written 09/26/10] — 4 straight losses, 6-12 in the past three weeks, .529 since the All-Star break — suggests that their third dynasty may be drawing to a close [but not quite, see below]. It would be unsurprising if that turns out to be so. Where are the replacements for Jeter, Posada, Pettitte, and Rivera, whose average age is 38? A-Rod is close behind, at 34, and not the A-Rod of a few years ago. Tex, at 30, is on the cusp of decline, and his numbers show it. Of the younger generation of position players, only Robinson Cano exudes star quality. Curtis Granderson is no Bernie Williams; Nick Swisher, no Paul O’Neill.

The only reliable starter is CC Sabathia. A.J. Burnett and Javier Vasquez don’t belong on a championship-calibre team. Phil Hughes isn’t convincing, despite his 17 wins. The bullpen reminds me of a rowboat in a hurricane. Even Mariano has become a question mark.

Given the evident dearth of outstanding young players, the end of the present dynasty seems to be in sight — or perhaps visible in the rear-view mirror. The 2009 World Series may have marked the end of Yankees Dynasty III.

Dynasty I lasted from 1921, the year of the Yankees’ first AL championship, to 1964, the year of their 29th AL championship. There were some “down” years sprinkled throughout the period — most notably, 1925, the year of the Babe’s big stomach ache, when the Yankees finished seventh in the days of the eight-team league. But the Yankees never went more than four seasons without a pennant, and finished below third (in eight- and ten-team leagues) only twice. Overall record in 44 seasons: 29 league championships and 20 World Series championships.

Dynasty II lasted only six seasons: 1976-1981. The Yankees led their division in four of those years, and wound up with the AL crown in 1981, despite an overall fourth-place finish, thanks to the split season (due to a players’ strike) and a post-season playoff to determine the division winner. Overall record in six seasons: 5 division championships, 4 league championships, and 2 World Series championships.

Dynasty III (on the current evidence) lasted 16 19 seasons: 1994-2009 2012. Overall record: 14 17 appearances in post-season play, 12 14 division championships, 7 league championships, and 5 World Series championships. (Don’t forget that in 1994 the Yankees had no opportunity to compete for a league or World Series championship because a players’ strike wiped out post-season play.) That’s a lot better than Dynasty II and a lot worse than Dynasty I.

In the following graph [updated to include the 2011-13 seasons], the black line indicates the Yankees’ finishes in the American League (1901-1968) or Eastern Division of the AL (1969-2013). The red, horizontal bars indicate the number of teams in the league or division, for each season. The blue shading highlights the years of the Yankees’ dynasties, to date. It looks like the end for Dynasty III — and end that coincides with the retirements of Mariano Rivera and Andy Pettite, the final declines of Jeter and A-Rod.

In the course of preparing the three preceding posts, I compiled the table below. Note that the American League’s overall record is slightly better than the National League’s. That’s because of the AL’s edge in interleague play, which continues into 2010.

Won-Lost records, 1901-2009
(franchise histories at bottom of table)
National League
Team	Games	Won	Lost	W-L%
Giants	16994	9070	7834	.537
Dodgers	16995	8841	8065	.523
Cardinals	17006	8774	8128	.519
Pirates	16993	8607	8292	.509
Cubs	17012	8545	8367	.505
Reds	17010	8484	8436	.501
Diamondbacks	1944	970	974	.499
Astros	7652	3812	3835	.498
Braves	16983	8168	8708	.484
Mets	7644	3655	3981	.479
Marlins	2686	1283	1403	.478
Nationals	6511	3098	3409	.476
Rockies	2692	1281	1411	.476
Phillies	16955	7830	9051	.464
Padres	6518	3008	3508	.462
Brewers	1943	889	1053	.458
NL totals	173538	86315	86455	.4996
American League
Team	Games	Won	Lost	W-L%
Yankees	16962	9575	7294	.568
Red Sox	16973	8730	8160	.517
Indians	16987	8622	8274	.510
Tigers	17013	8564	8356	.506
White Sox	16982	8540	8339	.506
Angels	7811	3887	3921	.498
Blue Jays	5224	2589	2632	.496
Athletics	16947	8189	8671	.486
Royals	6505	3143	3360	.483
Twins	16995	8138	8748	.482
Brewers	4570	2200	2367	.482
Orioles	16986	8013	8863	.475
Mariners	5223	2461	2760	.471
Rangers	7797	3657	4134	.469
Rays	1941	826	1115	.426
AL totals	174916	87134	86994	.5004
Franchise histories:
National League
Giants in San Francisco, 1958- ; in New York (also as Gothams), 1883-1957
Dodgers in Los Angeles, 1958 – ; in Brooklyn (also as Robins, Bridegrooms, Grooms), 1890-1957); previously in American Association (as Bridegrooms, Grays, Atlantics), 1884-1889
Cardinals in St. Louis (also as Perfectos, Browns), 1892- ; previously in American Association (as Browns, Brown Stockings), 1882-1891
Pirates in Pittsburgh (also as Alleghenys), 1887- ; previously in American Association (as Alleghenys), 1882-1886
Cubs in Chicago (also as Orphans, Colts, White Stockings), 1876-
Reds in Cincinnati (also as Redlegs), 1890- ; previously in American Association (as Red Stockings), 1882-1889
Diamondbacks in Arizona (Phoenix), 1998-
Astros in Houston (also as Colt .45’s), 1962-
Braves in Atlanta, 1966- ; in Milwaukee, 1953-1965; in Boston (also as Bees, Rustlers, Doves, Beaneaters, Red Caps), 1876-1952
Mets in New York, 1962-
Marlins in Florida (Miami), 1993-
Nationals in Washington, 2005- ; in Montreal (as Expos), 1969-2004
Rockies in Colorado (Denver), 1993-
Phillies in Philadelphia (also as Quakers), 1883-
Padres in San Diego, 1969-
Brewers in Milwaukee, 1998- (see AL entry for previous history)
American League
Yankees in New York (also as Highlanders), 1903- ; in Baltimore (as Orioles), 1901-1902
Red Sox in Boston (also as Americans), 1901-
Indians in Cleveland (also as Naps, Bronchos, Blues), 1901-
Tigers in Detroit, 1901-
White Sox in Chicago, 1901-
Angels in Anaheim, 1961- , but indentified variously as Los Angeles Angels of Anaheim, Anaheim Angels, California Angels, Los Angeles Angels
Blue Jays in Toronto, 1977-
Athletics in Oakland, 1968- ; in Kansas City, 1955-1967; in Philadelphia, 1901-1954
Twins in Minnesota (Minneapolis), 1961- ; in Washington (as Senators), 1901-1960
Royals in Kansas City, 1969-
Brewers in Milwaukee, 1970-1997; in Seattle (as Pilots), 1969
Orioles in Baltimore, 1954- ; in St. Louis (as Browns), 1902-1953; in Milwaukee (as Brewers), 1901
Rangers in Texas (Arlington), 1972- ; in Washington (as Senators) 1961-1971
Mariners in Seattle, 1977-
Rays in Tampa Bay (St. Petersburg, also as Devil Rays), 1998-

According to an article posted in the “Bullpen” at Baseball-Reference.com, the Pythagorean Theorem of Baseball

relates the number of runs a team has scored and surrendered to its actual winning percentage….

There are two ways of calculating Pythagorean Winning Percentage (W%). The more commonly used, and simpler version uses an exponent of 2 in the formula.

W%=[(Runs Scored)^2]/[(Runs Scored)^2 + (Runs Allowed)^2]

More accurate versions of the formula use 1.81 or 1.83 as the exponent.

W%=[(Runs Scored)^1.81]/[(Runs Scored)^1.81 + (Runs Allowed)^1.81]

An analysis of statistics available at Baseball-Reference.com, which include expected W%, yields the following straightforward version of the Pythagorean expectation:

W% = 1.8195*RS% – 0.4098, where

W% = games won/(games won + games lost),

RS% = runs scored/(runs scored + runs allowed), and

* indicates multiplication.

The Pythagorean formula used by Baseball-Reference.com bears a strong resemblance to the long-term (1901-2009) relationship between W% and RS%, which is:

W% = 1.8372*RS% – 0.4191

This equation is no longer accurate, however. Nor is any equation that neglects the evolution of the game through its six “modern” eras: Deadball (1901-1919), Lively Ball I (1920-1941), Wartime Lull (1942-1946), Lively Ball II (1947-1961), High Plateau (1962-1993), and Juiced Player (1994-2xxx). Here are the formulae for each of the six eras:

Deadball

W% = 1.7679 * RS% – 0.3843

Lively Ball I

W% = 1.8965 * RS% – 0.4482

Wartime Lull

W% = 1.7389 * RS% – 0.3686

Lively Ball II

W% = 1.8704*RS% – 0.4377

High Plateau

W% = 1.7521*RS% – 0.3760

Juiced Player

W% = 1.9882*RS% – 0.4940

This final equation seems like the one to use, until there is a marked change in the style of play. Results will vary from year to year, of course. Here, for example, is the equation for 2009:

W% = 1.9419*RS% – 0.4707

Related post: Explaining a Team’s W-L Record

In the preceding post, I identified six eras of “modern” baseball:

1901-1919 — Deadball (“modern”)

1920-1941 — Lively Ball I

1942-1946 — Wartime Lull

1947-1961 — Lively Ball II

1962-1993 — High Plateau

1994-2xxx — Juiced Player

These six eras have distinctive characters, which are captured in the following table:

				Change from 1901-1919
		Runs per	HR per	Add’l runs	Add’l HR	Runs per
Era	# Teams	game	game	per game	per game	add’l HR
1901-1919	16	7.84	0.30
1920-1941	16	9.69	0.97	1.85	0.67	2.76
1942-1946	16	8.14	0.88	0.30	0.58	0.52
1947-1961*	18	8.91	1.62	1.07	1.32	0.81
1962-1993**	26	8.37	1.56	0.53	1.26	0.42
1994-2009***	30	9.62	1.63	1.78	1.33	1.34
1994-2009	“old 16”	9.73
1901-2009	30	8.82
1901-2009	“old 16”	8.85
* 2 expansion teams in 1961
** 2 expansion teams in 1962; 4 in 1969; 2 in 1977; 2 in 1993
*** 2 expansion teams in 1998

Lively Ball Era I was the most dynamic era to date. There were more home runs than in the Deadball era, to be sure, but it is evident that much of the “small ball” action of the Deadball era carried over into Lively Ball I.

The Wartime Lull was just that. There were more home runs than in the Deadball era, but every home run netted only 0.52 runs on the scoreboard. Think of batters reaching base and mostly waiting around for a home run to be hit, usually to no avail.

The next two eras — Lively Ball II and High Plateau — saw a resurgence of home-run hitting, but run production didn’t return to the level of Lively Ball II. Again, there was a lot of waiting around for home runs, usually to no avail.

The era of the Juiced Player rivals (but falls short of) the dynamism of Lively Ball I. Yes, a lot more home runs per game (what would you expect?), but not quite the same number of runs per game.

I have always had the impression that baseball in the 1920s and 1930s was baseball at its exciting best: power added to the “small ball” wiles of the Deadball era. The numbers seem to confirm that impression.

EXTRA INNINGS:

The runs-per-game figures for the “old 16” teams — the franchises in existence from 1901 through 1960 — suggest that those teams have done better than the expansion upstarts. In fact, for the Juiced Player era (1994-2009), the “old 16” have a W-L record of .512.

But not all of the “old 16” have fared well. Here are the W-L rankings of the “old 16” for the period 1994-2009:

Rank (of 30)	Team	G	W	L	W-L%
1	NYY	2524	1514	1007	.601
2	ATL	2525	1456	1068	.577
3	BOS	2526	1409	1117	.558
4	CLE	2523	1353	1170	.536
5	STL	2525	1347	1176	.534
7	LAD	2526	1336	1190	.529
9	OAK	2524	1312	1212	.520
10	CHW	2527	1312	1212	.520
11	SFG	2526	1310	1215	.519
14	PHI	2526	1260	1266	.499
17	MIN	2525	1251	1273	.496
19	CIN	2530	1232	1295	.488
20	CHC	2524	1230	1294	.487
24	BAL	2525	1175	1347	.466
27	DET	2526	1108	1418	.439
28	PIT	2523	1091	1431	.433

“Old 16” teams occupy the top five spots and 10 of the top 15 spots. But Baltimore (13 straight losing seasons, 1998-2010), Detroit (12 straight losing seasons, 1994-2005), and Pittsburgh (18 straight losing seasons, 1993-2010) have turned in especially embarrassing performances.

It is generally thought that the lively ball era began in 1920. In that year, the number of home runs per major-league game jumped to 0.511, eclipsing the previous “modern” high of 0.411, set in 1911. But the home-run barrage was only beginning in 1920. It jumped to 0.762 per game in 1921 — nearly double the 1911 mark — and continued around a rising trend through the rest of the pre-World War II era:

Despite Babe Ruth’s dominance in the early years of the lively ball era — he hit almost 9 percent of ML home runs in 1920, and more than 6 percent in 1927 — it wasn’t until 1931 that the AL began to outslug the NL every year. But there was plenty of slugging to go around, as the peaks and high valleys of 1930-1941 attest. I attribute the higher home-run output of those years to arrival of a new generation of players, who were selected more often than not for their slugging ability and encouraged to cultivate that ability.

But the real lively ball eras were yet to come:

Following a lull from 1942 through 1946, the home-run barrage resumed in 1947, with the post-war return of slugging veterans and the influx of newcomers raised in the slugging tradition. The second lively ball era peaked in 1961. It subsided with the “era of the pitcher” and the first waves of expansion. But even at its lowest ebb in the 1970s and 1989s, the pace of home-run production exceeded the peaks of the first lively ball era, with only a few exceptions.

Then came 1994 and a third era. This one, sad to say, probably owed its existence not to a “juiced” baseball but to “juiced” baseball players. Given the crackdown on performance-enhancing substances, the rate of home-run production in 2010 (to date) has dropped to that of 1961 — when the “juice” in the game came from a performance-inhibiting substance known as alcohol.

I hereby declare the following eras:

1901-1919 — Deadball (“modern”)

1920-1941 — Lively Ball I

1942-1946 — Wartime Lull

1947-1961 — Lively Ball II

1962-1993 — High Plateau

1994-2xxx — Juiced Player

The induction of Andre Dawson into the Hall of Fame provides a new benchmark for admission:

• a career OPS+* of at least 119 and

• a career BA of at least .279

By that standard, there are 45 players (past and present) with substantial careers (at least 8,000 plate appearances) who deserve (or will deserve) membership in the Hall of Fame. Here they are, ranked by career OPS+ and then by career BA:

OPS+ rank	Player	OPS+	BA
1	Barry Bonds	181	.298
2	Frank Thomas	156	.301
3	Manny Ramirez	155	.313
4	Jeff Bagwell	149	.297
5	Edgar Martinez	147	.312
6	Alex Rodriguez	146	.303
7	Jason Giambi	143	.282
8	Vladimir Guerrero	143	.320
9	Chipper Jones	142	.306
10	Gary Sheffield	140	.292
11	Larry Walker	140	.313
12	Todd Helton	138	.324
13	Carlos Delgado	138	.280
14	Bob Johnson	138	.296
15	Will Clark	137	.303
16	Reggie Smith	137	.287
17	Sherry Magee	136	.291
18	Ken Griffey	135	.284
19	Fred McGriff	134	.284
20	Rafael Palmeiro	132	.288
21	Ken Singleton	132	.282
22	Bobby Abreu	130	.296
23	John Olerud	128	.295
24	Keith Hernandez	128	.296
25	Joe Torre	128	.297
26	Ellis Burks	126	.291
27	Bernie Williams	125	.297
28	Bobby Bonilla	124	.279
29	Rusty Staub	124	.279
30	Bob Elliott	124	.289
31	Jimmy Ryan	124	.308
32	Jeff Kent	123	.290
33	Tim Raines	123	.294
34	Cesar Cedeno	123	.285
35	Hal McRae	122	.290
36	Ed Konetchy	122	.281
37	Dave Parker	121	.290
38	Al Oliver	121	.303
39	George Van Haltren	121	.316
40	Harold Baines	120	.289
41	Paul O’Neill	120	.288
42	Jose Cruz	120	.284
43	Derek Jeter	119	.314
44	Mark Grace	119	.303
45	Stan Hack	119	.301

BA rank	Player	OPS+	BA
1	Todd Helton	138	.324
2	Vladimir Guerrero	143	.320
3	George Van Haltren	121	.316
4	Derek Jeter	119	.314
5	Manny Ramirez	155	.313
6	Larry Walker	140	.313
7	Edgar Martinez	147	.312
8	Jimmy Ryan	124	.308
9	Chipper Jones	142	.306
10	Alex Rodriguez	146	.303
11	Will Clark	137	.303
12	Al Oliver	121	.303
13	Mark Grace	119	.303
14	Frank Thomas	156	.301
15	Stan Hack	119	.301
16	Barry Bonds	181	.298
17	Jeff Bagwell	149	.297
18	Joe Torre	128	.297
19	Bernie Williams	125	.297
20	Bob Johnson	138	.296
21	Bobby Abreu	130	.296
22	Keith Hernandez	128	.296
23	John Olerud	128	.295
24	Tim Raines	123	.294
25	Gary Sheffield	140	.292
26	Sherry Magee	136	.291
27	Ellis Burks	126	.291
28	Jeff Kent	123	.290
29	Hal McRae	122	.290
30	Dave Parker	121	.290
31	Bob Elliott	124	.289
32	Harold Baines	120	.289
33	Rafael Palmeiro	132	.288
34	Paul O’Neill	120	.288
35	Reggie Smith	137	.287
36	Cesar Cedeno	123	.285
37	Ken Griffey	135	.284
38	Fred McGriff	134	.284
39	Jose Cruz	120	.284
40	Jason Giambi	143	.282
41	Ken Singleton	132	.282
42	Ed Konetchy	122	.281
43	Carlos Delgado	138	.280
44	Bobby Bonilla	124	.279
45	Rusty Staub	124	.279

___
* OPS+ is on-base percentage plus slugging average (OPS) adjusted for where and when a batter compiled his statistics.

Statistics derived from the Play Index at Baseball-Reference.com.

Are sluggers becoming more or less prevalent?

To answer that question, I went to the Play Index feature of Baseball-Reference.com. I was able to find (thanks to a paid subscription to Play Index) the number of players, by season, with an OPS+ statistic* of 150 or more, from 1901 through 2009. Dividing each season’s number by the number of major-league teams, I obtained the following result:

Observations:

1. There has been a slight but noticeable decline in the average number of players per team with an OPS+ of 150 or more, especially following the second round of expansion in 1969.

2. The surge from 1996 to 2002 probably marks the peak use of performance-enhancing drugs.

3. The decline resumed after 2002.

Thus, for whatever reason(s), slugging seems to be in decline.

__________
* Definition: “OPS+ is OPS [on-base plus slugging percentage] adjusted for the park and the league in which the player played,” where the league average for a given year is 100. Thus “An OPS+ of 150 or more is excellent and 125 very good, while an OPS+ of 75 or below is poor.”

Drawing on statistics available at Baseball-Reference.com, I have plotted complete games as a percentage of games started, by league and for both major leagues, at five-year intervals from 1904 through 2009. (It would have been too cumbersome and not worth the effort to have transcribed the statistics for every season from 1901 through 2010).

The result:

Observations:

The rise of complete games in the American League following the introduction of the designated hitter was a transitory phenomenon.

The statistics for the National League are therefore more indicative of long-term trends.

The complete game has been on the wane since the early 1900s, but the trend has accelerated since 1970. (The use of the logarithmic scale for the vertical axis highlights that acceleration.)

It is likely that the incidence of complete games has reached a minimum, at around three percent of games started. That is to say, the percentage is unlikely to drop further because there will always be those (infrequent) occasions on which a starter is still throwing well and has thrown fewer than 100 pitches as he goes into the eighth and ninth innings of a game in which his team is leading, tied, or only a run or two behind.

It has long been conventional wisdom in baseball that batters hit their peak in their late 20s and go into decline after the age of 30. But inasmuch as this conventional wisdom pre-dates the days of massive computerized databases and spreadsheets, can it be true, or is it the baseball equivalent of an old wives tale?

To answer that question, I went to the Play Index feature of Baseball-Reference.com. I was able to find (thanks to a paid subscription to Play Index) the career OPS+ statistic* for all inactive or retired players from 1901 through 2009 who had at least 3,000 plate appearances. As of yesterday, there were 1,416 such players. I selected 57 of them by the simple (and essentially random) method of picking #1 Babe Ruth (career OPS+ 207) and every 25th batter thereafter: #26 Jeff Bagwell (149), #51 Babe Herman (140, and so on, down to #1401 Bill Kellefer (63). The resulting sample represents great-to-poor batters, players in all eras from 1901 onward, and careers long, short (but not too short), and in between.

I indexed each player’s single-season OPS+ statistics to that player’s career-high OPS+. For example, Babe Ruth’s career looks like this:

Season	Age	OPS+	Indexed
1914	19	50	0.196
1915	20	189	0.741
1916	21	121	0.475
1917	22	162	0.635
1918	23	194	0.761
1919	24	219	0.859
1920	25	255	1.000
1921	26	239	0.937
1922	27	181	0.710
1923	28	239	0.937
1924	29	220	0.863
1925	30	137	0.537
1926	31	227	0.890
1927	32	226	0.886
1928	33	208	0.816
1929	34	193	0.757
1930	35	211	0.827
1931	36	218	0.855
1932	37	201	0.788
1933	38	176	0.690
1934	39	161	0.631
1935	40	118	0.463

After making the same computation for the other 56 batters, I plotted the indexed values for all batters against age, with the following result:

The ages at which the players peaked (index value of 1.00) range from 22 to 36, but the polynomial curve tells the tale: major-league batters tend to improve gradually as they approach ages 29-30, and then to decline gradually thereafter.

That is a broad generalization, based on a random sample of batters. Even within that sample, and certainly across the entire population of batters, there are many-many exceptions. Babe Ruth is a prominent exception. He peaked at age 25, by the measure of OPS+, declined somewhat, improved somewhat, and did not go into his final decline until the age of 37.

In any event, the conventional wisdom stands up to scrutiny, but (like conventional wisdom about many things) it is a rule of thumb, not an iron-clad law of behavior.
__________
* Definition: “OPS+ is OPS [on-base plus slugging percentage] adjusted for the park and the league in which the player played,” where the league average for a given year is 100. Thus “An OPS+ of 150 or more is excellent and 125 very good, while an OPS+ of 75 or below is poor.”

Since the advent of three-tiered postseason play in 1995, a league’s best team has seldom appeared in the World Series. Here’s the tally (National League teams listed first; * indicates winner of World Series):

1995 —
Atlanta Braves (division winner; .625 W-L, best record in NL)*
Cleveland Indians (division winner; .694 W-L, best record in AL)

1996 —
Atlanta Braves (division winner; .593, best in NL)
New York Yankees (division winner; .568, second-best in AL)*

1997 —
Florida Marlins (wild-card team; .568, second-best in NL)*
Cleveland Indians (division winner; .534, fourth-best in AL)

1998–
San Diego Padres (division winner; .605 third-best in NL)
New York Yankees (division winner, .704, best in AL)*

1999–
Atlanta Braves (division winner; .636, best in NL)
New York Yankees (division winner; .605, best in AL)*

2000–
New York Mets (wild-card team; .580, fourth-best in NL)
New York Yankees (division winner; .540, fifth-best in AL)*

2001–
Arizona Diamondbacks (division winner; .568, fourth-best in NL)*
New York Yankees (division winner; .594, third-best in AL)

2002–
San Francisco Giants (wild-card team; .590, fourth-best in NL)
Anaheim Angels (wild-card team; .611, third-best in AL)*

2003–
Florida Marlines (wild-card team; .562, third-best in NL)*
New York Yankees (division winner; .623, best in AL)

2004–
St. Louis Cardinals (division winner; .648, best in NL)
Boston Red Sox (wild-card team; .605, second-best in AL)*

2005–
Houston Astros (wild-card team; .549, third-best in NL)
Chicago White Sox (division winner; .611, best in AL)*

2006–
St. Louis Cardinals (division winner; .516, fifth-best in NL)*
Detroit Tigers (wild-card team; .586, third-best in AL)

2007–
Colorado Rockies (wild-card team; .552, second-best in NL)
Boston Red Sox (division winner; .593, tied for best in AL)*

2008–
Philadelphia Phillies (division winner; .568, second-best in NL)*
Tampa Bay Rays (division winner; .599, second-best in AL)

2009–
Philadelphia Phillies (division winner; .574, second-best in NL)
New York Yankees (division winner; .636, best in AL)*

There you have it. The last year in which the World Series featured each league’s best team was 1999. The only other time was in 1995.

Of the 15 Series from 1995 through 2009, 9 were won by the inferior team, as measured by W-L record. Division winners opposed each other in only 6 of the 15 Series.

Wild-card teams appeared in 8 of the 15 Series. With an all wild-card Series in 2002, wild-card teams have occupied almost a third of the 30 Series slots — 9 of 30.

As I have said, the winner of the World Series can claim nothing more than having been the better team over a span of four to seven games.

According to Baseball-Reference.com:

The Pythagorean Theorem of Baseball is a creation of Bill James which relates the number of runs a team has scored and surrendered to its actual winning percentage, based on the idea that runs scored/runs allowed is a better indicator of a team’s (future) performance than a team’s actual winning percentage. This results in a formula which is referred to as Pythagorean Winning Percentage….

There are two ways of calculating Pythagorean Winning Percentage (W%). The more commonly used, and simpler version uses an exponent of 2 in the formula.

W%=[(Runs Scored)^2]/[(Runs Scored)^2 + (Runs Allowed)^2]

More accurate versions of the formula use 1.81 or 1.83 as the exponent.

W%=[(Runs Scored)^1.81]/[(Runs Scored)^1.81 + (Runs Allowed)^1.81]

Expected W-L can then be obtained by multiplying W% by the team’s total number of games played, then rounding off….

The rationale behind Pythagorean Winning Percentage is that, while winning as many games as possible is still the ultimate goal of a baseball team, a team’s run differential (once a sufficient number of games have been played) provides a better idea of how well a team is actually playing. Therefore, barring personnel issues (injuries, trades), a team’s actual W-L record will approach the Pythagorean Expected W-L record over time, not the other way around. Expected W-L is almost always within 3 games of actual W-L at the end of a season (although a recent exception is the 2005 and 2007 Arizona Diamondbacks, who both beat their expected W-L by 11 games). Deviations from expected W-L are often attributed to the quality of a team’s bullpen, or more dubiously, “clutch play”; many sabermetrics advocates believe the deviations are the result of luck and random chance.

I agree with those who say that deviations reflect the quality of a team’s bullpen. A more precise formula can be obtained by regressing winning percentage on two explanatory variables: RFA (runs scored/[runs scored + runs allowed]) and saves recorded by a team’s bullpen. The result for the American League in 2008:

W-L percentage (expressed as a decimal fraction) = -0.44595 + 1.66556 x RFA + 0.002747 x saves

Adjusted R-squared: 0.899; standard error: 0.022 (i.e., 2.2 percentage points); t-statistics on the intercept and coefficients: -4.246, 7.319, 3.763 (all significant above the 0.99 level).

That is, the average American League team (RFA = .506, saves = 41) compiled a W-L percentage of .510. (The AL beat the NL in interleague play, thus enabling the AL as a whole to compile a better-than-.500 average.)

According to the Pythagorean formula, the LA Angels were the lucky recipients of 11 extra wins in 2008; that is, the formula underestimates the Angels’ 2008 wins by 11. The regression equation, on the other hand, underestimates the Angels’ 2008 wins by only 2. Generally, the regression equation (indicated by blue) gives much better results than the Pythagorean formula (indicated by black):

“Luck” is a catch-all term for unexplained variance. It shouldn’t be thrown around as if it has real meaning. In this case, the evidence suggests that a decisive factor in a team’s W-L record is the quality of its bullpen — especially the quality of its closers.

Way back in September 2004, before the Montreal Expos became the Washington Nationals, I wrote:

To succeed financially, the new Washington team must draw well from the Maryland and Virginia suburbs. Attendance will be high for a few years, because the closeness of major-league baseball will be a novelty to fans who’ve had to trek to Baltimore to see the increasingly hapless Orioles. But suburbanites’ allegiance to the new Washington team won’t survive more than a few losing seasons — and more than a few seem likely, given the Expos’ track record. As the crowds wane, suburbanites will become increasingly reluctant to journey into the city. And, so, the taxpayers of D.C. (and perhaps the taxpayers of the nation) are likely to be stuck with an expensive memento of false civic pride.

I’m not sure about this year’s attendance, but the trend is almost certain to be downward, given the Nats steady dive toward the bottom of the National League. Here are the Nats’ W-L records from 2005 through yesterday:

2005 – .500 (5th of 5 in their division; tied for 9th in their 16-team league)

2006 – .438 (5th of 5 in their division; 14th in the league)

2007 – .451 (4th of 5 in their division; tied for 11th in the league)

2008 – .366 (5th of 5 in their division; last in the league)

2009. – .345 (5th of 5 in their division; last in the league)

As I’ve said before, D.C. isn’t a baseball town. The teams are jinxed by their non-fans.

Greg Maddux, who is about to announce his retirement from baseball, is a cinch for election to the Hall of Fame: 355 wins, .610 winning average, ERA+ of 132. But Maddux, like recently-retired Mike Mussina, shouldn’t be ranked with the “immortals” — the 16 Hall of Fame pitchers whose excellence, in my view, ranks them above their peers. (See this post and this post for relevant background.)

Maddux had only two 20-win seasons, which is why he isn’t an “immortal” pitcher, in my book. Roger Clemens, Maddux’s contemporary, had six 20-win seasons (in addition to his 354 wins, .658 winning average, ERA+ of 143), which would make him an “immortal” but for the strong suspicion that his career totals were inflated by steroids and HGH. (It is, by the way, a strong suspicion that cannot be confirmed by statistical evidence.)

P.S. (12/08/08) The election of Joe Gordon to the Hall of Fame is a joke, by my reckoning.

I once opined that a

Hall of Fame [starting] pitcher will have

• at least 300 wins

• or, at least 250 wins and an ERA+ of 120 or higher. (Go here and scroll down for the definition of ERA+.)

• or, at least 200 wins and a W-L average of .600 or better and an ERA+ of 120 or higher.

I opined, further, that an ” ‘immortal’ pitcher will have at least 250 wins, a winning average of at least .600, and an ERA+ of at least 120.”

Well, it turns out that, by my definition, Mike Mussina qualifies as an “immortal”: 270 wins, a winning average of .638, and an ERA+ of 123. Not so fast.

Mussina, who has just announced his retirement, deserves to be in the Hall of Fame; I have no quibble with his qualifications on that score. But Mussina doesn’t strike me as an “immortal,” which is an honor that I would reserve for these starting pitchers:

Pete Alexander
John Clarkson
Bob Feller
Lefty Grove
Carl Hubbell
Walter Johnson
Tim Keefe
Christy Mathewson
Kid Nichols
Jim Palmer
Eddie Plank
Charley Radbourn
Tom Seaver
Cy Young

Accordingly, I must add another criterion for “immortality” among starting pitchers: at least five seasons with 20 or more wins. Mussina had only one such season: his last.

If — in this era of the relief pitcher — there is never another “immortal” starting pitcher, so be it. Tom Seaver will then have the honor of being the last of the breed.