Wherein your humble blogger gets to the bottom of the Monty Hall problem, sorts out the conflicting solutions, and declares that the standard solution is the right solution, but not to the Monty Hall problem as it’s usually posed.
THE MONTY HALL PROBLEM AND THE TWO “SOLUTIONS”
The Monty Hall problem, first posed as a statistical puzzle in 1975, has been notorious since 1990, when Marilyn vos Savant wrote about it in Parade. Her solution to the problem, to which I will come, touched off a controversy that has yet to die down. But her solution is now widely accepted as the correct one; I refer to it here as the standard solution.
This is from the Wikipedia entry for the Monty Hall problem:
The Monty Hall problem is a brain teaser, in the form of a probability puzzle (Gruber, Krauss and others), loosely based on the American television game show Let’s Make a Deal and named after its original host, Monty Hall. The problem was originally posed in a letter by Steve Selvin to the American Statistician in 1975 (Selvin 1975a), (Selvin 1975b). It became famous as a question from a reader’s letter quoted in Marilyn vos Savant‘s “Ask Marilyn” column in Parade magazine in 1990 (vos Savant 1990a):
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?
Here’s a complete statement of the problem:
1. A contestant sees three doors. Behind one of the doors is a valuable prize, which I’ll denote as $. Undesirable or worthless items are behind the other two doors; I’ll denote those items as x.
2. The contestant doesn’t know which door conceals $ and which doors conceal x.
3. The contestant chooses a door at random.
4. The host, who knows what’s behind each of the doors, opens one of the doors not chosen by the contestant.
5. The door chosen by the host may not conceal $; it must conceal an x. That is, the host always opens a door to reveal an x.
6. The host then asks the contestant if he wishes to stay with the door he chose initially (“stay”) or switch to the other unopened door (“switch”).
7. The contestant decides whether to stay or switch.
8. The host then opens the door finally chosen by the contestant.
9. If $ is revealed, the contestant wins; if x is revealed the contestant loses.
One solution (the standard solution) is to switch doors because there’s a 2/3 probability that $ is hidden behind the unopened door that the contestant didn’t choose initially. In vos Savant’s own words:
Yes; you [the contestant] should switch. The first [initially chosen] door has a 1/3 chance of winning, but the second [other unopened] door has a 2/3 chance.
The other solution (the alternative solution) is indifference. Those who propound this solution maintain that there’s a equal chance of finding $ behind either of the doors that remain unopened after the host has opened a door.
As it turns out, the standard solution doesn’t tell a contestant what to do in a particular game. But the standard solution does point to the right strategy for someone who plays or bets on a large number of games.
The alternative solution accurately captures the unpredictability of any particular game. But indifference is only a break-even strategy for a person who plays or bets on a large number of games.
EXPLANATION OF THE STANDARD SOLUTION
The contestant may choose among three doors, and there are three possible ways of arranging the items behind the doors: S x x; x $ x; and x x $. The result is nine possible ways in which a game may unfold:
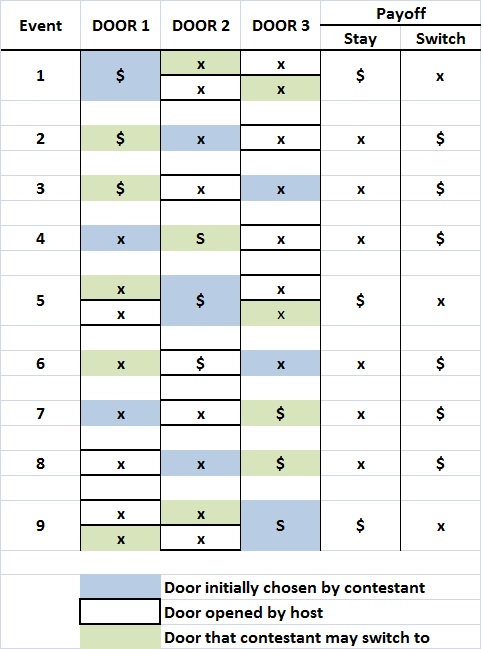
Events 1, 5, and 9 each have two branches. But those branches don’t count as separate events. They’re simply subsets of the same event; when the contestant chooses a door that hides $, the host must choose between the two doors that hide x, but he can’t open both of them. And his choice doesn’t affect the outcome of the event.
It’s evident that switching would pay off with a win in 2/3 of the possible events; whereas, staying with the original choice would off in only 1/3 of the possible events. The fractions 1/3 and 2/3 are usually referred to as probabilities: a 2/3 probability of winning $ by switching doors, as against a 1/3 probability of winning $ by staying with the initially chosen door.
Accordingly, proponents of the standard solution — who are now legion — advise the individual (theoretical) contestant to switch. The idea is that switching increases one’s chance (probability) of winning.
A CLOSER LOOK AT THE STANDARD SOLUTION
There are three problems with the standard solution:
1. It incorporates a subtle shift in perspective. The Monty Hall problem, as posed, asks what a contestant should do. The standard solution, on the other hand, represents the expected (long-run average) outcome of many events, that is, many plays of the game. For reasons I’ll come to, the outcome of a single game can’t be described by a probability.
2. Lists of possibilities, such as those in the diagram above, fail to reflect the randomness inherent in real events.
3. Probabilities emerge from many repetitions of the kinds of events listed above. It is meaningless to ascribe a probability to a single event. In case of the Monty Hall problem, many repetitions of the game will yield probabilities approximating those given in the standard solution, but the outcome of each repetition will be unpredictable. It is therefore meaningless to say that a contestant has a 2/3 chance of winning a game if he switches. A 2/3 chance of winning refers to the expected outcome of many repetitions, where the contestant chooses to switch every time. To put it baldly: How does a person win 2/3 of a game? He either wins or doesn’t win.
Regarding points 2 and 3, I turn to Probability, Statistics and Truth (second revised English edition, 1957), by Richard von Mises:
The rational concept of probability, which is the only basis of probability calculus, applies only to problems in which either the same event repeats itself again and again, or a great number of uniform elements are involved at the same time. Using the language of physics, we may say that in order to apply toe theory of probability we must have a practically unlimited sequence of uniform observations. (p. 11)
* * *
In games of dice, the individual event is a single throw of the dice from the box and the attribute is the observation of the number of points shown by the dice. In the same of “heads or tails”, each toss of the coin is an individual event, and the side of the coin which is uppermost is the attribute. (p. 11)
* * *
We must now introduce a new term…. This term is “the collective”, and it denotes a sequence of uniform events or processes which differ by certain observable attributes…. All the throws of dice made in the course of a game [of many throws] from a collective wherein the attribute of the single event is the number of points thrown…. The definition of probability which we shall give is concerned with ‘the probability of encountering a single attribute [e.g., winning $ rather than x ] in a given collective [a series of attempts to win $ rather than x ]. (pp. 11-12)
* * *
[A] collective is a mass phenomenon or a repetitive event, or, simply, a long sequence of observations for which there are sufficient reasons to believe that the relative frequency of the observed attributed would tend to a fixed limit if the observations were indefinitely continued. The limit will be called the probability of the attribute considered within the collective [emphasis in the original]. (p. 15)
* * *
The result of each calculation … is always … nothing else but a probability, or, using our general definition, the relative frequency of a certain event in a sufficiently long (theoretically, infinitely long) sequence of observations. The theory of probability can never lead to a definite statement concerning a single event. The only question that it can answer is: what is to be expected in the course of a very long sequence of observations? It is important to note that this statement remains valid also if the calculated probability has one of the two extreme values 1 or 0 [emphasis added]. (p. 33)
To bring the point home, here are the results of 50 runs of the Monty Hall problem, where each result represents (i) a random initial choice between Door 1, Door 2, and Door 3; (ii) a random array of $, x, and x behind the three doors; (iii) the opening of a door (other than the one initially chosen) to reveal an x; and (iv) a decision, in every case, to switch from the initially chosen door to the other unopened door:

What’s relevant here isn’t the fraction of times that $ appears, which is 3/5 — slightly less than the theoretical value of 2/3. Just look at the utter randomness of the results. The first three outcomes yield the “expected” ratio of two wins to one loss, though in the real game show the two winners and one loser would have been different persons. The same goes for any sequence, even the final — highly “improbable” (i.e., random) — string of nine straight wins (which would have accrued to nine different contestants). And who knows what would have happened in games 51, 52, etc.
If a person wants to win 2/3 of the time, he must find a game show that allows him to continue playing the game until he has reached his goal. As I’ve found in my simulations, it could take as many as 10, 20, 70, or 300 games before the cumulative fraction of wins per game converges on 2/3.
That’s what it means to win 2/3 of the time. It’s not possible to win a single game 2/3 of the time, which is the “logic” of the standard solution as it’s usually presented.
WHAT ABOUT THE ALTERNATIVE SOLUTION?
The alternative solution doesn’t offer a winning strategy. In this view of the Monty Hall problem, it doesn’t matter which unopened door a contestant chooses. In effect, the contestant is advised to flip a coin.
As discussed above, the outcome of any particular game is unpredictable, so a coin flip will do just as well as any other way of choosing a door. But randomly selecting an unopened door isn’t a good strategy for repeated plays of the game. Over the long run, random selection means winning about 1/2 of all games, as opposed to 2/3 for the “switch” strategy. (To see that the expected probability of winning through random selection approaches 1/2, return to the earlier diagram; there, you’ll see that $ occurs in 9/18 = 1/2 of the possible outcomes for “stay” and “switch” combined.)
Proponents of the alternative solution overlook the importance of the host’s selection of a door to open. His choice isn’t random. Therein lies the secret of the standard solution — as a long-run strategy.
WHY THE STANDARD SOLUTION WORKS IN THE LONG RUN
It’s commonly said by proponents of the standard solution that when the host opens a door, he gives away information that the contestant can use to increase his chance of winning that game. One nonsensical version of this explanation goes like this:
- There’s a 2/3 probability that $ is behind one of the two doors not chosen initially by the contestant.
- When the host opens a door to reveal x, that 2/3 “collapses” onto the other door that wasn’t chosen initially. (Ooh … a “collapsing” probability. How exotic. Just like Schrödinger’s cat.)
Of course, the host’s action gives away nothing in the context of a single game, the outcome of which is unpredictable. The host’s action does help in the long run, if you’re in a position to play or bet on a large number of games. Here’s how:
- The contestant’s initial choice (IC) will be wrong 2/3 of the time. That is, in 2/3 of a large number of games, the $ will be behind one of the other two doors.
- Because of the rules of the game, the host must open one of those other two doors (HC1 and HC2); he can’t open IC.
- When IC hides an x (which happens 2/3 of the time), either HC1 and HC2 must conceal the $; the one that doesn’t conceal the $ conceals an x.
- The rules require the host to open the door that conceals an x.
- Therefore, about 2/3 of the time the $ will be behind HC1 or HC2, and in those cases it will always be behind the door (HC1 or HC2) that the host doesn’t open.
- It follows that the contestant, by consistently switching from IC to the remaining unopened door (HC1 or HC2), will win the $ about 2/3 of the time.
The host’s action transforms the probability — the long-run frequency — of choosing the winning door from 1/2 to 2/3. But it does so if and only if the player or bettor always switches from IC to HC1 or HC2 (whichever one remains unopened).
You can visualize the steps outlined above by looking at the earlier diagram of possible outcomes.
That’s all there is. There isn’t any more.
